天才数学家又出成果!他解决了困扰数学界80年的Duffin-Schaeffer猜想,连陶哲轩都夸他厉害!
作者|超模君 来源|超级数学建模(ID:supermodeling)
每三年才评选一次的数论界最高奖“柯尔奖”,在今年颁给了詹姆斯.梅纳德(James Maynard),以表彰他对素数理论的诸多贡献。
柯尔奖:美国数学学会授奖,分为数论奖和代数奖。它不是国际化奖项,只颁发给学会成员,且在美国期刊上发表过出色文章,被誉为数论界的最高奖。
说起詹姆斯.梅纳德,这就是一位“天才少年”,他在22岁取得了剑桥大学的硕士学位,26岁获得了牛津大学的博士学位,33岁就已经成为牛津大学的一名研究教授。

孪生素数猜想
也许大家看到“柯尔奖”觉得有些陌生,超模君也是在2014年才开始对它印象深刻,因为那一年这个奖项颁给了华裔数学家张益唐,用以表彰他证明了弱化版本孪生素数猜想。
孪生素数猜想是数论中著名的尚未解决的问题,相差2的一对素数即是孪生素数,比如:3和5,5和7,11和13.......
它可以被描述为:存在无穷多个素数P,并且对每个P而言,P+2这个数也是素数。
弱孪生素数猜想:对所有自然数K,存在无穷多个素数对(P,P+2K)。当K=1时是孪生素数猜想,当K等于其他自然数时就称为弱孪生素数猜想。
关于素数,故事要追溯到两千多年前,古希腊数学家欧几里得给出了自己的证明:素数有无穷多个。
从小就爱数学的我们,可以很快把100以内的素数列举出来:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73 ,79 ,83,89,97
这些素数起初看起来很密集,但是随着素数的增大,彼此之间的距离渐渐变远,而孪生素数的出现距离也跟着变得更远......
素数分布距离没有规律,要想找到一个大素数,加上分解和验证,都需要大量的计算。千百年来,孪生素数猜想成为了数学家无法攻克的难题。
2013年,58岁的张益唐成功证明了存在无数对孪生素数,而且其中每一对的孪生素数之差不超过7000万,把孪生素数的距离从无限变成了有限。
张益唐凭借着这个证明,获得了数论界最高奖“柯尔奖”。就在他证明“孪生素数猜想”不久,年仅26岁的詹姆斯.梅纳德将猜想中素数间隔的上限由7000万降到了600,极大优化了张益唐的证明结果。
詹姆斯.梅纳德的证明方法一问世就震惊了数学界,华裔数学家陶哲轩感慨地说:
“说实话,他的描述方式实际上比我的更干净,事实证明他的方法还略强。”

其实,证明的过程并不是一帆风顺的,詹姆斯.梅纳德后来回忆说:
“很长一段时间,我们都在这一问题上一筹莫展,寸步难行,任何新见解的出现都会让人激动不已。”
但是,他最终还是做到了,这就是数学家的坚持,超模君佩服!
Duffin-Schaeffer猜想
就在詹姆斯.梅纳德获得“柯尔奖”前不久,他又成功证明了一个困扰数学界80年的难题Duffin-Schaeffer猜想。

Duffin-Schaeffer猜想:1941年由物理学家Richard Duffin和数学家Albert Schaeffer提出,它是数论中关于丢番图逼近中一个重要猜想。
所谓丢番图逼近,是数论的一个分支,研究的是用有理数逼近实数。
我们可以简单的理解为用“分数”的形式逼近某个数,达成“近似表达”。
比如π是一个无理数,它可以笼统的用
这个简单的分数完成近似表达。
无理数,有着无限不循环的小数,不能准确的表达为分数的形式。一些重要的无理数有了自己的专门符号,如 等,而更多的则以无名的形式散布在我们的生活当中。
等,而更多的则以无名的形式散布在我们的生活当中。
那么类似的无理数,还有没有可能也用分数的形式进行表达呢?甚至逐渐逼近,更加精确?
于是这个问题就变成了:不能准确表达,那么到底能精确到什么程度?
詹姆斯.梅纳德在他和同伴的证明论文中,把这个猜想描述为:
“存在一个简单的判定条件,可以判断你能够找出几乎所有数的近似值,或几乎找不到任何数的近似值。”
来自牛津大学的本.格林教授谈到这个问题时说道:
“很难写下![]() 的定义,人们通常取而代之的是寻找
的定义,人们通常取而代之的是寻找
的特定近似值,一种常见方法就是利用有理数来近似。”
千百年来,数学家们为此绞尽脑汁,不停计算,不断逼近:

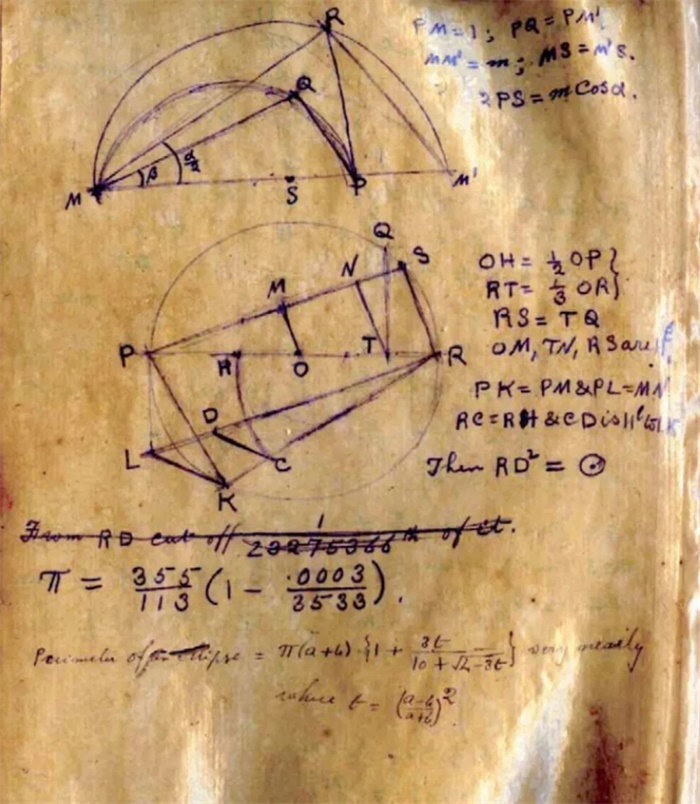
1913年,拉马努金在手稿内用355/113当作![]() 的近似值
的近似值
其实,如果你对误差大小不太在意,找到一个近似值很容易。但是数学家,他们对自己热爱的往往表现出过分的执着。
1837年,数学家迪利克雷发现了无理数用有理数近似时的误差大小法则:
对于每一个无理数都存在无限多个分数可以越来越精确地近似表达该无理数。
换句话说:每个近似分数和无理数之间的误差不超过1除以分数分母的平方,随着分母的增大,存在无限多的分数值和越来越接近。

詹姆斯.梅纳德团队针对Duffin-Schaeffer猜想选择了一种新的证明方法。选出了一个无限长的整数数列,这个数列可以包括任何你想要的整数,充当分母。

在数轴上任一区间内都存在无限个无理数
允许你为数列上每一个分母定义一个误差值,例如要求分母为3的分数误差为0.02,或者分母为5的分数允许误差0.01。

选好误差值
如果误差可以覆盖整条数轴,那么所有的无理数都可以被这组分母近似表达。

如果选出的分数群相互之间靠的很近,误差区间有很多重叠的地方,就意味着有很多无理数不能被覆盖。

在Duffin-Schaeffer猜想中,有一个关键点在于:
对于一组拥有很多小公共质因数的分母,找出一种方法来精确量化它们可以近似表达的无理数集之间重叠的程度。
这也是这个猜想80年来难住了数学家们的原因。现在,梅纳德和他的同伴用了一种新的方法解决了这个问题。
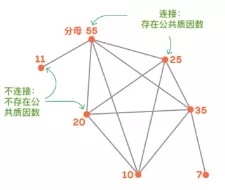
这张图将拥有大量公共质因数的分母分别连接起来,数学家可以通过分析图内存在的结构来证明:即使分母之间存在大量质因数,Duffin-Schaeffer猜想依然成立。
詹姆斯.梅纳德对数字有着超乎寻常的热爱。在他眼里,这些无理数中的小数点后的数字就像一只只小动物,而这个小数点就是一个牢笼,牢笼困住了它们。

他说:“我非常幸运,得到了支持和鼓励,从小我就对数学产生了浓厚的兴趣。我的父母总是鼓励我遵循自己的兴趣,而我的老师则允许我发展自己的独立品味。”
他这种对数字与生俱来的敏感,使他在数论界大放异彩。
2014年,詹姆斯.梅纳德获得SASTRA拉曼努金奖2015年,获得伦敦数学学会怀特海奖
2016年,获得欧洲数学学会奖
2014年至2016年间的Compositio奖2018年,国际数学家大会担任演讲嘉宾
2020年,获得美国柯尔奖
数论一直以来被大众认为是枯燥的,又因为在实际问题中缺乏实用性,属于数学中比较冷门的一支。

当詹姆斯.梅纳德谈到这些数字时,他眼睛里绽放着璀璨的光亮。
在得知自己获得“柯尔奖”后,詹姆斯.梅纳德回应说:“我为解析数论领域目前正被许多人提出的新想法而振兴感到兴奋,希望这一奖项可以激励更多的数学家继续保持势头,并发现有关素数的更多发现。”
参考文章:
https://www.quantamagazine.org/new-proof-settles-how-to-approximate-numbers-like-pi-20190814/
作者简介:超模君,数学教育与生活自媒体博主,新晋理工科奶爸。出版过《芥子须弥 · 大科学家的小故事》;《数学之旅·闪耀人类的54个数学家》。后续数学文化创意多多,欢迎关注认识!
编者按:本文转载自微信公众号:超级数学建模(ID:supermodeling)











